故事尾音

喜欢推导也喜欢被推倒

0%

K 近邻分类

发表于 更新于 Valine：


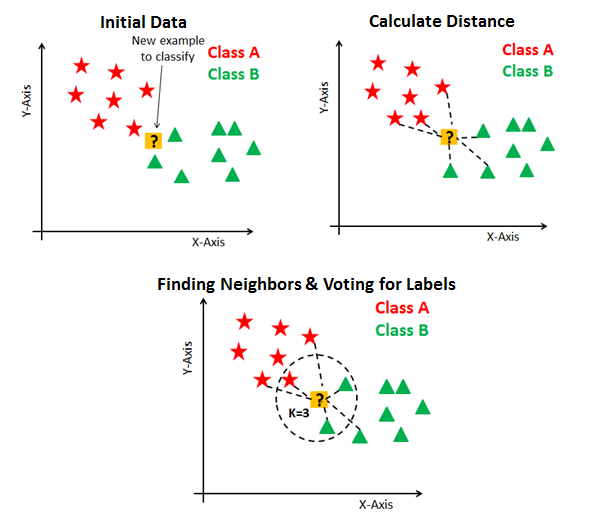
核心思想：基于距离的模板匹配
KNN 是一种判别模型，即支持分类问题，也支持回归问题，是一种非线性模型，天然支持多分类，而且没有训练过程。

KNN 算法的三要素

三个要素分别是：

  • K 值的选取
  • 分类决策规则（多数投票法）
  • 距离度量的方式，一般有欧氏距离，曼哈顿距离，闵可夫斯基距离等

K 值的选取


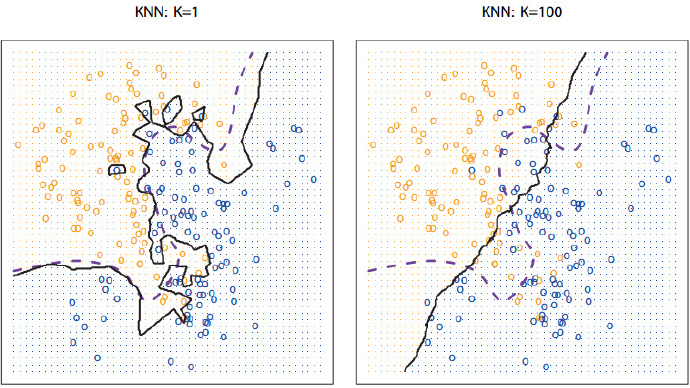
在上图中，紫色虚线是贝叶斯决策边界线，也是最理想的分类边界，黑色实线是 KNN 的分类边界。
K 值的选取没有固定经验，一般根据样本分布选择一个较小的值，可以通过交叉验证确定；K 值较小意味着整体模型变复杂，容易过拟合；K 值增大意味着模型变简单。另外，K 的取值尽量要取奇数，以保证在计算结果最后会产生一个较多的类别，如果取偶数可能会产生相等的情况，不利于预测。

KNN 的实现

暴力实现

KD 树实现

KNN 的优缺点

KNN 的主要优点有：
1） 理论成熟，思想简单，既可以用来做分类也可以用来做回归
2） 可用于非线性分类
3） 训练时间复杂度比支持向量机之类的算法低，仅为 O (n)
4） 和朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感
5） 由于 KNN 方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN 方法较其他方法更为适合
6）该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分

KNN 的主要缺点有：
1）计算量大，尤其是特征数非常多的时候
2）样本不平衡的时候，对稀有类别的预测准确率低
3）KD 树，球树之类的模型建立需要大量的内存
4）使用懒散学习方法，基本上不学习，导致预测时速度比起逻辑回归之类的算法慢
5）相比决策树模型，KNN 模型可解释性不强

代码实现

numpy 版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
import numpy as np
from math import sqrt
from collections import Counter
from matplotlib import pyplot as plt

class KNNClassifier:

    def __init__(self, k):
        """初始化kNN分类器"""
        assert k >= 1, "k must be valid"
        self.k = k
        self._X_train = None
        self._y_train = None

    def fit(self, X_train, y_train):
        """根据训练数据集X_train和y_train训练kNN分类器"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"
        assert self.k <= X_train.shape[0], \
            "the size of X_train must be at least k."

        self._X_train = X_train
        self._y_train = y_train
        return self

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self._X_train is not None and self._y_train is not None, \
                "must fit before predict!"
        assert X_predict.shape[1] == self._X_train.shape[1], \
                "the feature number of X_predict must be equal to X_train"

        y_predict = [self._predict(x) for x in X_predict]
        return np.array(y_predict)

    def _predict(self, x):
        """给定单个待预测数据x，返回x的预测结果值"""
        assert x.shape[0] == self._X_train.shape[1], \
            "the feature number of x must be equal to X_train"

        distances = [sqrt(np.sum((x_train - x) ** 2))
                     for x_train in self._X_train]
        nearest = np.argsort(distances)

        topK_y = [self._y_train[i] for i in nearest[:self.k]]
        votes = Counter(topK_y)

        return votes.most_common(1)[0][0]

    def __repr__(self):
        return "KNN(k=%d)" % self.k

if __name__ == '__main__':


    X = [[3.393533211, 2.331273381],
         [3.110073483, 1.781539638],
         [1.343808831, 3.368360954],
         [3.582294042, 4.679179110],
         [2.280362439, 2.866990263],
         [7.423436942, 4.696522875],
         [5.745051997, 3.533989803],
         [9.172168622, 2.511101045],
         [7.792783481, 3.424088941],
         [7.939820817, 0.791637231]
         ]
    y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]

    X_train = np.array(X)
    y_train = np.array(y)

    x_predict = np.array([8.093607318, 3.36571514])

    plt.scatter(X_train[y_train == 0, 0], X_train[y_train == 0, 1], color='g')
    plt.scatter(X_train[y_train == 1, 0], X_train[y_train == 1, 1], color='r')
    plt.scatter(x_predict[0],x_predict[1], color='b')

    plt.show()

    model = KNNClassifier(k=3)
    model.fit(X_train,y_train)
    result = model.predict(np.expand_dims(x_predict,0))
    print("class:",result)


tensorflow版本
kd树版本

面试常见问题

  • 简述一下 KNN 算法的原理
  • KNN 算法有哪些优点和缺点？
  • 不平衡的样本可以给 KNN 的预测结果造成哪些问题，有没有什么好的解决方式？
  • 为了解决 KNN 算法计算量过大的问题，可以使用分组的方式进行计算，简述一下该方式的原理。
  • 什么是欧氏距离和曼哈顿距离？
    欧式距离：曼哈顿距离：闵可夫斯基距离:

  • KNN 中的 K 如何选取的？
    ①k 值较小时，相当于用较小的邻域中的训练实例进行预测，近似误差会减小，只有与输入实例很相近的样本才会对预测结果起作用。估计误差会增大，整体模型会变得复杂，容易过拟合。
    ②选取较大的 k 值是，相当于用较大的邻域中的训练实例进行预测，可以减少学习的估计误差，但是近似误差会增大，因为离输入实例较远的样本也对预测结果起作用，容易使预测发生错误。k 过大导致模型变得简单。
    ③在选取 k 上，一般取比较小的值，并采用交叉验证法进行调优。
    K 的取值尽量要取奇数，以保证在计算结果最后会产生一个较多的类别，如果取偶数可能会产生相等的情况，不利于预测。

  • 什么是 KD 树？

  • KD 树建立过程中切分维度的顺序是否可以优化？
  • KD 树每一次继续切分都要计算该子区间在需切分维度上的中值，计算量很大，有什么方法可以对其进行优化？
支持一根棒棒糖！