香农（1916 年 4 月 30 日－2001 年 2 月 26 日），美国数学家、电子工程师和密码学家，被誉为信息论的创始人。1948 年，香农发表了划时代的论文 —— 通信的数学原理，在这部著作中，他提出了比特数据，证明了信息是可以被量化的，并阐述了如何在保证准确率的前提下用数字编码对信息进行压缩和传输。

信息量和信息熵

我们都知道，物质、能量、信息是构成现实世界的三大要素。其中物质和能量的度量由物理学和化学中的牛顿定律、热力学定律和质能方程解释的很好了。唯独剩下信息，如何度量信息呢？

信息量

我们常说信息的多少，这其实就是一种粗略的度量。举个例子

• 太阳从东方升起了 —— 没有什么信息
• 李彦宏被泼水了，还问了”what’s your problem”—— 信息量很大，开始吃瓜

为什么说第二个事情信息量大呢？本质上是因为第二个时间出现的概率低。由此我们把事件出现的概率和时间的信息关联起来了：事情的概率越低，事件的信息量越大。

信息熵

这就话的意思是说生活中的事情总会朝着最坏的方向发展。生活不但不会自行解决问题，甚至还会逐渐变得更糟糕和复杂。这背后的原因就是：熵。
信息熵其实是信息量的期望。

二分类交叉熵

我们假设要训练一个拥有多个输入变量的神经元：输入 $x_1, x_2, \ldots$ ，权重 $w_1, w_2, \ldots$ ，偏置为 $b$ ：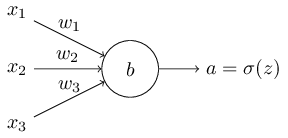

神经元的输出为 $a = \sigma (z)$ ，这里 $z = \sum_j w_j x_j+b$ ，我们定义这个神经元的交叉熵代价函数为：

$$\begin{eqnarray} C = -\frac{1}{n} \sum_x \left[y \ln a + (1-y ) \ln (1-a) \right]\end{eqnarray}$$

这里 $n$ 是训练数据的个数，这个加和覆盖了所有的训练输入 $x$ ， $y$ 是期望输出。注意这里用于计算的 $a$ 也是经过 $sigmoid$ 激活的，取值范围在 0 到 1 之间。

当输出 y 为 0 的时候，上面的式子变为： $-\ln (1-a)$ , 图像如下。可以看出当神经网络的输出也为 0 的时候 loss 最小，趋向于 1 的时候 loss 变大。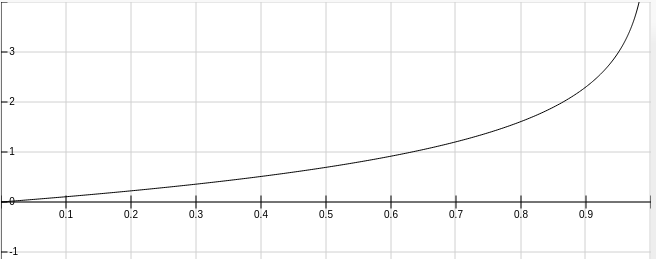

当输出 y 为 1 的时候，上面的式子变为：$-\ln (a)$ , 图像如下。可以看出当神经网络的输出也为 1 的时候 loss 最小，趋向于 0 的时候 loss 变大。

多分类交叉熵

$$softmax(s_i) = \frac{e^{s_i} }{\sum_{j=1}^{N}e^{s_j} } \qquad (i=1,\cdots,N)$$ $$\frac{\partial L}{\partial y_{j}}=-\sum_{j} \frac{\hat{y}_{j}}{y_{j}}$$