故事尾音

推荐系统整体流程

• 多路召回：首先召回阶段是会配置召回的请求个数，通常会根据每路召回的后验表现设置动态配比，或者是根据业务的需求进行设置。所有的召回并发请求并设置 timeout，防止系统雪崩。
• 所有的召回结果 merge。
• 过滤：系统整体的黑名单，以及 by user 的黑名单过滤都可以在此处实现。
• 去重：此处通常都是简单的指纹去重，不做特别精细的多样性去重（比如相似新闻通常在排序后做）。(过滤和去重都是为了减少后续系统的压力，防止浪费算力进行后续步骤。)
• 粗排后截断。当然粗排也可以放在每个召回队列中做，也是根据业务而定。
• 进行精排。
• 排序后的 rerank 处理，包括多样性去重，产品的特殊 boost 逻辑等。

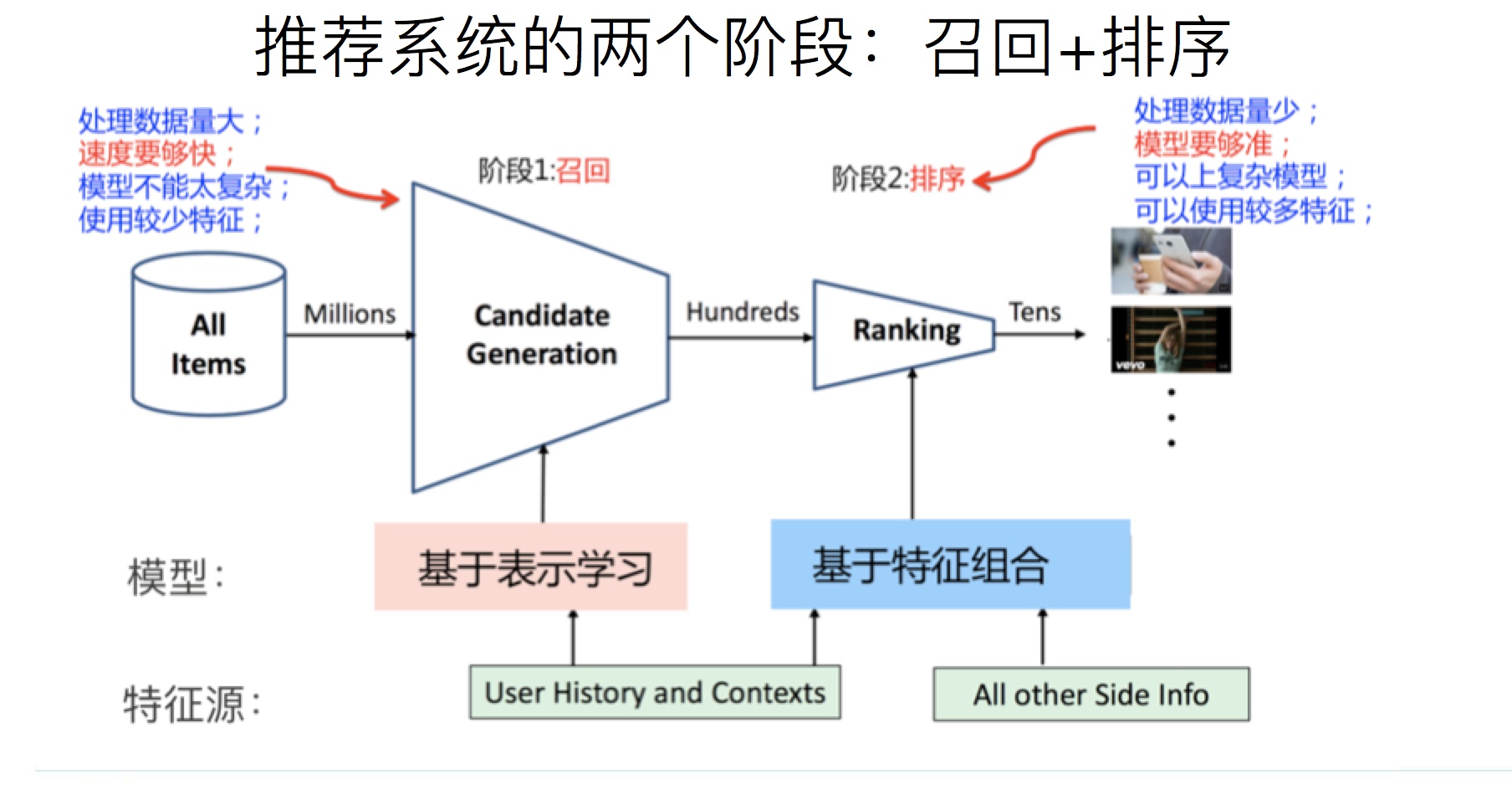
什么是召回

召回系统，本质上是个信息漏斗，负责快速从海量信息中筛选出有价值的信息，缩小排序算法的搜素范围；也负责将多路召回的数据，进行信息融合，最后得到一个精简的候选集。

召回的特性

处理的数据量非常大，速度要求快，所有使用的模型和特征都不能太复杂。

召回的重要性

• 奠基性：后续流程，基于召回数据展开
• 桥接性：建立用户和内容的桥梁
• 决定性：召回质量决定推荐质量

一个简单的 TFIDF 做文档检索，还可以继续加一些功能：

• [ ] 增加评估指标
• [ ] 增加新的模型，例如 BM25

实现效果：

通过 PowerShell 安装 OpenSSH

来自微软官方文档。 若要使用 PowerShell 安装 OpenSSH，请首先以管理员身份启动 PowerShell。 若要确保 OpenSSH 功能可以安装，请执行以下操作：

1
2
3
4
5
6
7
8
9
10

# 输入这句话

Get-WindowsCapability -Online | ? Name -like 'OpenSSH*'

# This should return the following output:

Name  : OpenSSH.Client~~~~0.0.1.0
State : NotPresent
Name  : OpenSSH.Server~~~~0.0.1.0
State : NotPresent

Step0：搭建深度学习环境

• Doker 搭建深度学习环境：https://www.cnblogs.com/bingmang/p/9813686.html
• Pycharm 远程连接服务器：https://www.cnblogs.com/zhuminghui/p/10947930.html
• 服务器使用 screen 后台运行程序：https://sunyanhust.github.io/post/fu-wu-qi-shi-yong-screen-hou-tai-yun-xing-cheng-xu/

📻音乐

• 音乐搜索器: 多站合一音乐搜索解决方案
• 果汁音乐

🔮搜索

• 虫部落
• 果汁搜索
• 小鸡词典：网络流行语
• wikihow：生活维基百科

📚融合 BN 加速推理

批归一化（Batch Normalization）因其可以加速神经网络训练、使网络训练更稳定，而且还有一定的正则化效果，所以得到了非常广泛的应用。但是，在推理阶段，BN 层一般是可以完全融合到前面的卷积层的，而且丝毫不影响性能。
参考文章：深度学习推理时融合 BN, 轻松获得约 5% 的提速
代码：keras 的暂时没有找到，有空可以写写

思路:

1. 先判断正负数
2. 将这个数转成字符串再转成字符数组
3. 将数组的首尾元素交换（注意正负）
4. 将字符数组转成字符串再转成整数（注意转换后的数是否超出 int 的取值范围）
5. 将这个整数返回

1
2
3
4
5
6
7
8
9
10
11

class Solution:
    def reverse(self, x: int) -> int:
        if x <0:
            res = -int("".join(list(str(-x))[::-1]))
        else:
            res = int("".join(list(str(x))[::-1]))
        
        if -2**31<=res<2**31-1:
            return res
        else:
            return 0

这道题本身如果通过暴力遍历的话也是很容易解决的，时间复杂度在 O (n2)，由于哈希查找的时间复杂度为 O (1)，所以可以利用哈希容器 map 降低时间复杂度 (这里使用 python 的字典)。

方法 1：两重循环

会报超时错误

1
2
3
4
5

def two_sum(nums, target):
    for i, n in enumerate(nums):
        for j, m in enumerate(nums):
            if target - n == m and i!=j:
                return [i,j]

方法 2：两遍 Hash

1
2
3
4
5

def two_sum(nums, target):
    dct = dict(zip(nums, range(len(nums))))
    for i, n in enumerate(nums) and i!=dct[target - n]:
        if target - n in dct:
            return [dct[target - n], i]

时间复杂度：O (n2)
空间复杂度：O (n)

方法 2：一遍 Hash (边循环边查字典)

1
2
3
4
5
6

def two_sum(nums, target):
    dct = {}
    for i, n in enumerate(nums):
        if target - n in dct:
            return [dct[target - n], i]
        dct[n] = i

时间复杂度：O (n2)
空间复杂度：O (n)