DIN 排序模型

论文

《Deep Interest Network for Click-Through Rate Prediction》

本文收录于 KDD18，来自于阿里妈妈的精准定向检索及基础算法团队。文章的创新点主要有三个：

Deep Interest Network（DIN）—— 通过一个局部激活单元（local activation unit）来自适应地从用户历史行为中学习他对于某个广告的兴趣。
Mini-batch Aware Regularization —— 即一个针对 mini-batch SGD 进行优化的 L2 norm 正则项，通过近似减少了计算量。
一个数据自适应的激活函数，对 PReLU 的 indicator function 进行修改，并取名为 Dice。

背景

Deep Interest Network (DIN) 是盖坤大神领导的阿里妈妈的精准定向检索及基础算法团队，在 2017 年 6 月提出的。它针对电子商务领域 (e-commerce industry) 的 CTR 预估，重点在于充分利用 / 挖掘用户历史行为数据中的信息。

数据特征： 针对互联网电子商务领域，数据特点：Diversity、Local Activation。
针对问题：用户有多个兴趣爱好，访问了多个 good_id，shop_id。为了降低纬度并使得商品店铺间的算术运算有意义，我们先对其进行 Embedding 嵌入。那么我们如何对用户多种多样的兴趣建模那？使用 Pooling 对 Embedding Vector 求和或者求平均。同时这也解决了不同用户输入长度不同的问题，得到了一个固定长度的向量。这个向量就是用户表示，是用户兴趣的代表。但是，直接求 sum 或 average 损失了很多信息。所以稍加改进，针对不同的 behavior id 赋予不同的权重，这个权重是由当前 behavior id 和候选广告共同决定的。这就是 Attention 机制，实现了 Local Activation。
DIN 的解决方案：
1. 使用 用户兴趣分布 (Diversity) 来表示用户多种多样的兴趣爱好
2. 使用 Attention 机制 来实现 Local Activation
3. 针对模型训练，提出了 Dice 激活函数，自适应正则 (Adaptive Regulation)，显著提升了模型性能与收敛速度

Diversity： 用户在访问电商网站时会对多种商品都感兴趣。也就是用户的兴趣非常的广泛。

Local Activation： 由于用户兴趣的多样性，只有部分历史数据会影响到当次推荐的物品是否被点击，而不是所有的历史记录。

Diversity 体现在年轻的母亲的历史记录中体现的兴趣十分广泛，涵盖羊毛衫、手提袋、耳环、童装、运动装等等。而爱好游泳的人同样兴趣广泛，历史记录涉及浴装、旅游手册、踏水板、马铃薯、冰激凌、坚果等等。

Local activation 体现在，当我们给爱好游泳的人推荐 google (护目镜) 时，跟他之前是否购买过薯片、书籍、冰激凌的关系就不大了，而跟他游泳相关的历史记录如游泳帽的关系就比较密切。

模型结构

Base 模型

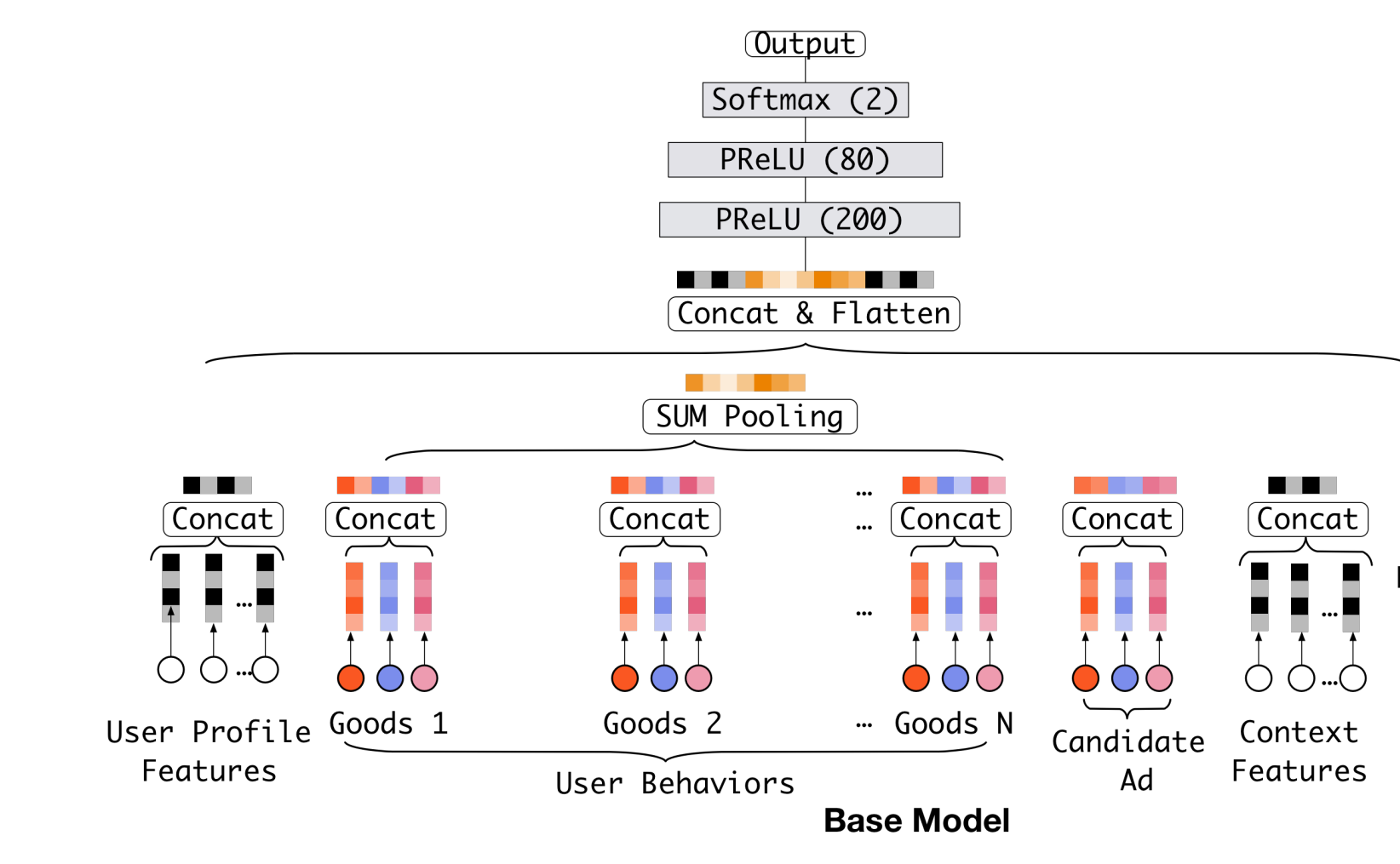
Base Model 首先把 one-hot 或 multi-hot 特征转换为特定长度的 embedding，作为模型的输入，然后经过一个 DNN 得到最终的预估值。

特别地，针对 multi-hot 的特征，做了一次 element-wise + 的操作，这里其实就是 sum-pooling，这样，不管特征中有多少个非 0 值，经过转换之后的长度都是一样的。multi-hot 特征也称为多值离散特征，比如：用户在 YouTube 上看的视频和搜索过的视频。无论是看过的还是搜索过的，都不止一个，但是相对于所有的视频来说，看过和搜索过的数量都太小了 (非常稀疏)。在电子商务上的例子就是：用户购买过的 good_id 有多个，购买过的 shop_id 也有多个，而这也直接导致了每个用户的历史行为 id 长度是不同的。

模型的基本过程如下：

在输入上面加一层 embeding 层，把最原始高维度、稀疏的数据转换为低维度的实值表示上 (dense vector)。
增加多个全连接层，学习特征之间的非线性关系。 Sparse Features -> Embedding Vector -> MLPs -> Output

从基准模型的结构图中可以看出，无论候选商品是什么，用户的 Embedding 值均不会发生改变。用户的历史行为中的商品 Embedding 数据对用户的 Embedding 的贡献力度是一样的，然而这与实际情况并不符合，因为每个用户的兴趣是多样性的。

举个例子：某用户购买过 “外套”、“手机”、“洗面奶”、“小说” 等，当用户计划购买 “耳机” 的时候，历史行为中的 “手机” 自然比其他商品对本次决策的贡献更大一些；当计划购买裤子的时候，历史行为中的 “外套” 自然比其他商品对本次决策的贡献更大一些。

在实际情况下，基准模型的效果存在待改进的空间，由此阿里提出了基于用户兴趣的深层网络（DIN 模型）。

DIN 模型

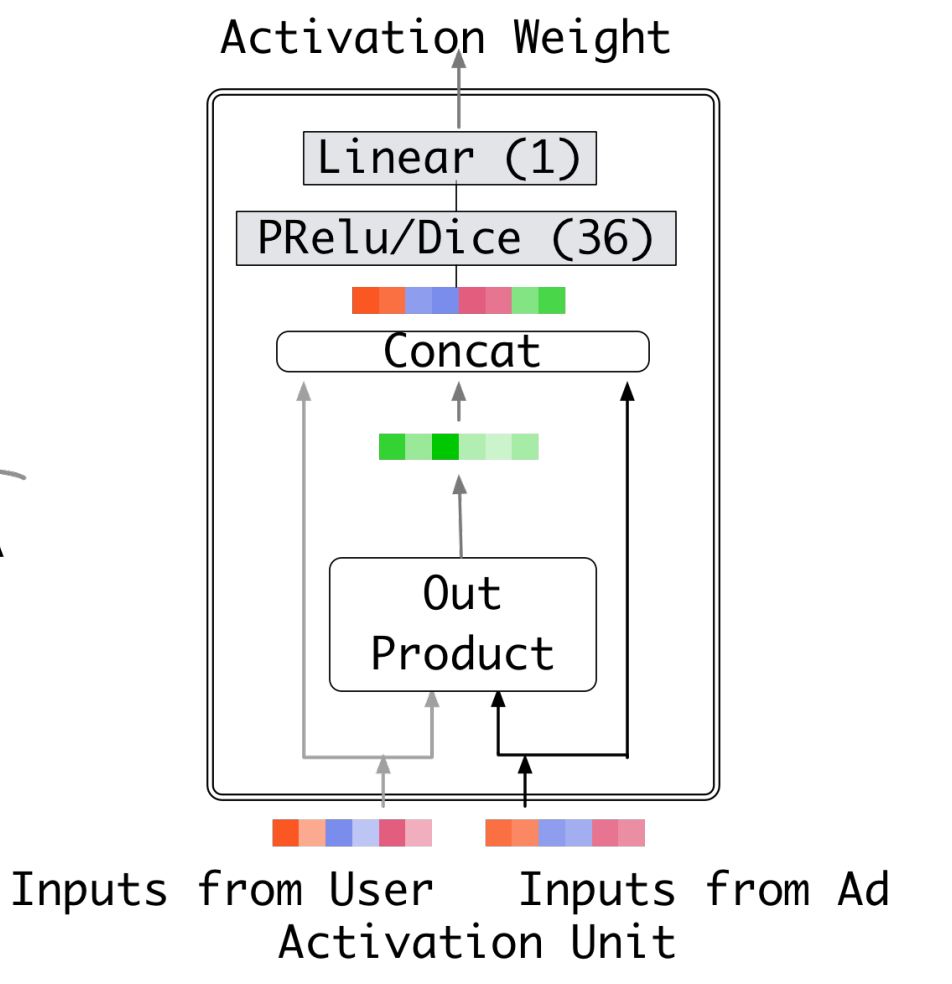
DIN 的模型结构中增加了 Activation Unit 模块，该模块主要提取当前候选商品与历史行为中的商品的权重值。输入包括两个部分：

一个是原始的用户行为 Embedding 向量、商品 Embedding 向量；
另外一个是两者 Embedding 向量经过外积计算后得到的向量，和两者 Embedding 向量差值得到的向量。

外积 + embedding 拼接有点类似于 FM 的思想，构造所谓的 “一阶” 和 “二阶交叉” 特征，其实就是通过一种方式来在原始 embedding 之上构建一些行为和广告的交叉特征，再通过全连接层对信息进一步整合并得到对应的权重。

$g(V_i, V_a)=PReLU([V_i, V_a, V_i \otimes V_a]) * W$

DIN 模型在基准模型的基础上，增加了注意力机制，就是模型在对候选商品预测的时候，对用户不同行为的注意力是不一样的。“相关” 的行为历史看重一些，“不相关” 的历史甚至可以忽略。在 DIN 场景中，针对不同的候选广告需要自适应地调整 User Representation。也就是说：在 Embedding Layer -> Pooling Layer 得到用户兴趣表示的时候，依据给定 Ad，通过计算用户历史行为与该给定 Ad 的相关性，赋予不同的历史行为不同的权重，实现局部激活。从最终反向训练的角度来看，就是根据当前的候选广告，来反向的激活用户历史的兴趣爱好，赋予不同历史行为不同的权重。

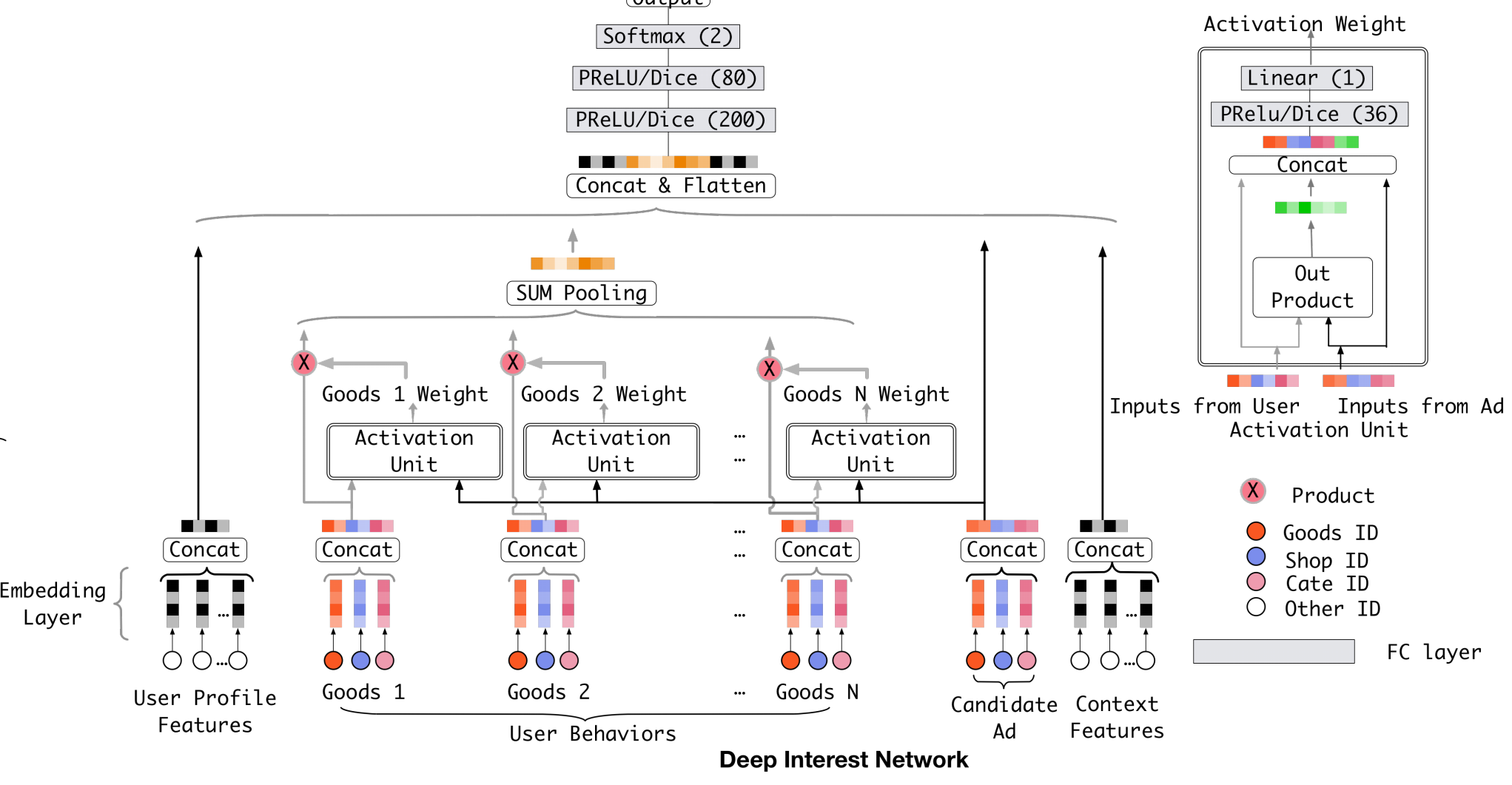
上面这张图是是 DIN 的网络结构。左边是它整体的一个结构，右边是激活单元的一个详细说明（这里的激活单元就是上文中说的得到权重的方式）。我们先看左边的整体结构。最下面是 embedding 层，将高维稀疏的原始数据映射为低维稠密向量。embedding 后的特征分为四部分：用户画像特征，用户行为特征，广告特征和上下文特征，其中用户行为特征会通过激活单元以及 sum pooling 得到一个处理后的针对当前广告的总体兴趣向量（因为激活单元的输出是一个标量，所以这里其实就是对用户行为特征的加权求和）。将这四部分拼接后，通过两层全连接层和一层 softmax 就可以得到最后的概率值。

训练技术

Mini-batch Aware Regularization

CTR 中输入稀疏而且维度高，论文中举出 ID 类特征的维度为 0.6 billion，若是不添加任何正则的话，模型表现在一个 epoch 之后快速下降。通常的做法是加入 L1、L2 防止过拟合，但这种正则方式对于工业级 CTR 数据不适用，结合其稀疏性及上亿级的参数，以 L2 正则化为例，需要计算每个 mini-batch 下所有参数的 L2-norm，参数上升至亿级之后计算量太大，不可接受。

用户数据符合长尾定律 long-tail law，也就是说很多的 feature id 只出现了几次，而一小部分 feature id 出现很多次。这在训练过程中增加了很多噪声，并且加重了过拟合。

对于这个问题一个简单的处理办法就是：直接去掉出现次数比较少的 feature id。但是这样就人为的丢掉了一些信息，导致模型更加容易过拟合，同时阈值的设定作为一个新的超参数，也是需要大量的实验来选择的。

因此，阿里提出了自适应正则的做法，即：

针对 feature id 出现的频率，来自适应的调整他们正则化的强度；
对于出现频率高的，给与较小的正则化强度；
对于出现频率低的，给予较大的正则化强度。

提出 mini-batch aware regularizer（小批量感知正则化器），只计算出现在 mini-batch 中的稀疏特征参数的 L2-norm（即只计算 mini-batch 中非零项的 L2-norm）。它可以节省具有大量参数的深度网络上正则化的大量计算，并且有助于避免过度拟合。

Dice: Data Dependent Activation Function

本文设计了一种 data adaptive activation function，命名为 Dice：

$p(s) = \frac{1}{1+e^{- \frac{s-E[s]}{\sqrt{Var[s] + \epsilon}}}} \label{eq1}$ $f(s)= p(s) s + (1-p(s)) as$

和 BN 类似，在训练时，$E [s]， $Var[s]$分别是每个mini-batch输入的均值和方差；在测试时，$E[s]，$ Var [s]$ 随着数据进行移动求平均。$\epsilon$ 是一个小常数项，设定为 $10^{-8}$。

公式 $\eqref {eq1}$ 也可以进一步的用 BN 来表示：

$p(s) = sigmoid(BN(s))$

Dice 的代码实现如下：

def Dice(_x, axis=-1, epsilon=0.000000001, name='dice', training=True):
    alphas = tf.get_variable('alpha_'+name, _x.get_shape()[-1],
            initializer=tf.constant_initializer(0.0),
            dtype=tf.float32)
    inputs_normed = tf.layers.batch_normalization(
            inputs=_x, 
            axis=axis, 
            epsilon=epsilon, 
            center=False, 
            scale=False, 
            training=training)
    x_p = tf.sigmoid(inputs_normed)
    return alphas * (1.0 - x_p) * _x + x_p * _x

优点：

根据数据分布灵活调整阶跃变化点，具有 BN 的优点 (解决 Internal Covariate Shift)，原论文称效果好于 Parametric ReLU。

缺点：

具有 BN 的缺点，大大加大了计算复杂度。

评价指标 GAUC

因为推荐系统的排序是个性化的，不同用户的排序结果不太好比较，这可能导致全局 auc 并不能反映真实情况。论文采用的 GAUC 实现了用户级别的 AUC 计算，在单个用户 AUC 的基础上，按照点击次数或展示次数进行加权平均，消除了用户偏差对模型的影响，更准确的描述了模型的表现效果（论文里面叫 An variation of user weighted AUC，用户加权 AUC）。

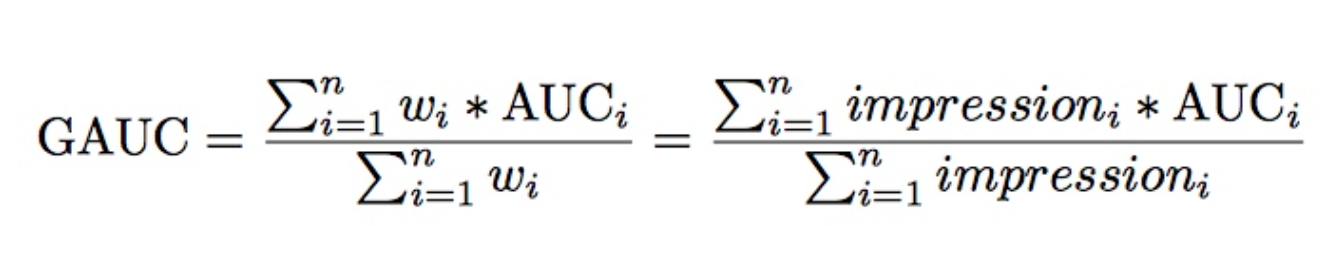
其中 n 是用户数， $impression$ 和 $AUC_{i}$ 是第 $i$ 个用户的 impression 数和对应 AUC。一般计算时，会过滤掉单个用户全是正样本或负样本的情况。

impression：就是曝光数

AUC 是要分用户看的，我们的模型的预测结果，只要能够保证对每个用户来说，他想要的结果排在前面就好了。假设有两个用户 A 和 B，每个用户都有 10 个商品，10 个商品中有 5 个是正样本，我们分别用 TA，TB，FA，FB 来表示两个用户的正样本和负样本。也就是说，20 个商品中有 10 个是正样本。假设模型预测的结果大小排序依次为 TA，FA，TB，FB。如果把两个用户的结果混起来看，AUC 并不是很高，因为有 5 个正样本排在了后面，但是分开看的话，每个用户的正样本都排在了负样本之前，AUC 应该是 1。显然，分开看更容易体现模型的效果，这样消除了用户本身的差异。

但是上文中所说的差异是在用户点击数即样本数相同的情况下说的。还有一种差异是用户的展示次数或者点击数，如果一个用户有 1 个正样本，10 个负样本，另一个用户有 5 个正样本，50 个负样本，这种差异同样需要消除。GAUC 的计算，不仅将每个用户的 AUC 分开计算，同时根据用户的展示数或者点击数来对每个用户的 AUC 进行加权处理，进一步消除了用户偏差对模型的影响。通过实验证明，GAUC 确实是一个更加合理的评价指标。

复习一下 AUC 的计算：正例排在负例之前的概率。假设总共有（m+n）个样本，其中正样本 m 个，负样本 n 个，总共有 m n 个样本对，计数，正样本预测为正样本的概率值大于负样本预测为正样本的概率值记为 1，累加计数，然后除以 m n 就是 AUC 的值。

AUC 的计算：

def naive_auc(labels,preds):
    """
　　　先排序，然后统计有多少正负样本对满足：正样本预测值>负样本预测值, 再除以总的正负样本对个数
     复杂度 O(NlogN), N为样本数
    """
    n_pos = sum(labels)
    n_neg = len(labels) - n_pos
    total_pair = n_pos * n_neg
 
    labels_preds = zip(labels,preds)
    labels_preds = sorted(labels_preds,key=lambda x:x[1])
    accumulated_neg = 0
    satisfied_pair = 0
    for i in range(len(labels_preds)):
        if labels_preds[i][0] == 1:
            satisfied_pair += accumulated_neg
        else:
            accumulated_neg += 1
 
    return satisfied_pair / float(total_pair)

GAUC 的计算：

from collections import defaultdict
from sklearn.metrics import roc_auc_score
import numpy as np

def cal_group_auc(labels, preds, user_id_list):
    """Calculate group auc"""

    if len(user_id_list) != len(labels):
        raise ValueError(
            "impression id num should equal to the sample num," \
            "impression id num is {0}".format(len(user_id_list)))
    group_score = defaultdict(lambda: [])
    group_truth = defaultdict(lambda: [])
    for idx, truth in enumerate(labels):
        user_id = user_id_list[idx]
        score = preds[idx]
        truth = labels[idx]
        group_score[user_id].append(score)
        group_truth[user_id].append(truth)

    group_flag = defaultdict(lambda: False)
    for user_id in set(user_id_list):
        truths = group_truth[user_id]
        flag = False
        for i in range(len(truths) - 1):
            if truths[i] != truths[i + 1]:
                flag = True
                break
        group_flag[user_id] = flag

    impression_total = 0
    total_auc = 0

    for user_id in group_flag:
        if group_flag[user_id]:
            auc = roc_auc_score(np.asarray(group_truth[user_id]), np.asarray(group_score[user_id]))
            total_auc += auc * len(group_truth[user_id])
            impression_total += len(group_truth[user_id])
    group_auc = float(total_auc) / impression_total
    group_auc = round(group_auc, 4)
    return group_auc

if __name__=='__main__':
     a=[1,2,1,2]
     b=[0.6,0.7,0,0]
     c=[1,1,0,0]
     d=np.array([[1],[1],[0],[0]])
     print(d)
     print(list(_flatten(d.tolist())))
     print(cal_group_auc(list(_flatten(d.tolist())),b,a))

实验结果

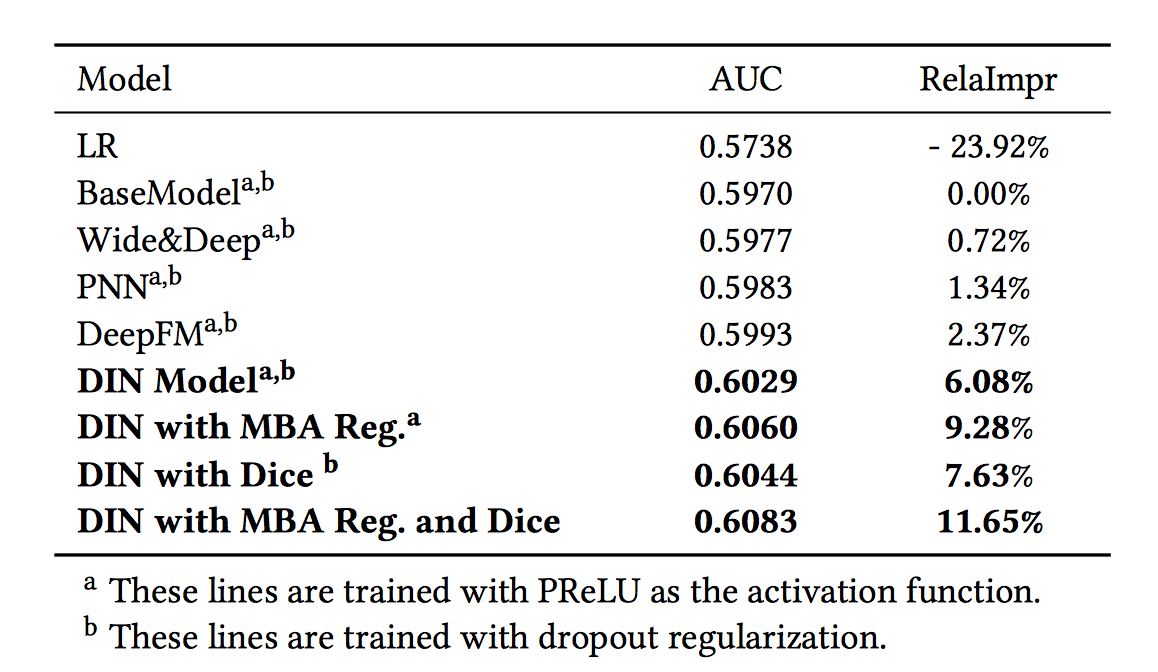
文章在公开数据集上进行了大量且细致的离线实验用以证明 DIN 模型的效果，具体可以参考论文中的表述。这里主要关注的是 DIN 模型的线上实验表现，因为该模型最终是要部署到线上真实环境中的，所以作为相关领域的从业人员，我也是更加关注该模型在 A/B Test 中的表现。文章指出相较于 Base 模型，DIN 模型表现十分突出，线上 CTR 增长 %10，RPM 增长 3.8%，在 CTR 预估领域百分之零点几的 CTR 增长都会带来巨大的增长，所以足以见得 DIN 模型的效果还是非常出色的，该模型也成为了阿里妈妈新一代的 CTR 预估模型。